[BOJ] 나이트의 이동(7562) - PYTHON

입력으로 체스판의 크기 M * M, 나이트의 시작 위치, 이동하고자 하는 위치가 주어진다. 이때 나이트가 목적지까지 가는데 걸리는 최소 이동 횟수를 구하는 문제다.

시간 복잡도: O(M^2)

7562번: 나이트의 이동

---

풀이 방법

나이트가 한번 이동할 때 갈 수 있는 위치는 다음과 같다.

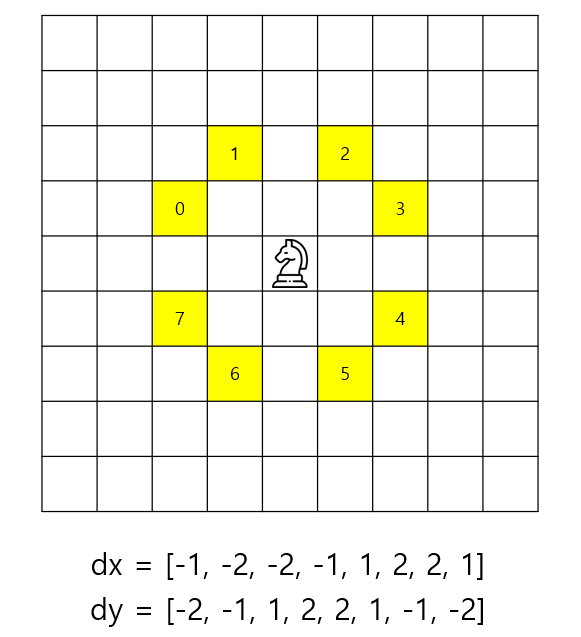
총 8위치로 이동할 수 있으며 그때의 x, y좌표 변화는 위의 식과 같다. (체스판의 숫자는 dx, dy배열에서의 index)

체스판의 각 위치에 대응하는 M * M 크기의 2차원 배열을 선언하고, 값으로 나이트가 이동하는 데 걸리는 최솟값을 저장하면, 모든 위치에 대해 나이트가 이동하는 데 걸리는 최솟값을 구할 수 있다. 이때 나이트가 이동할 수 있는 위치를 Queue에 넣고 위치를 하나씩 빼면서 거리를 저장하는 BFS(Breadth First Search)로 문제를 해결할 수 있다.

---

코드

import sys
from collections import deque
 
input = sys.stdin.readline
 
N = int(input())
dx = [-1, -2, -2, -1, 1, 2, 2, 1]
dy = [-2, -1, 1, 2, 2, 1, -1, -2]
 
for _ in range(N):
    M = int(input())
    arr = [[False for i in range(M)] for j in range(M)]
    sx, sy = map(int, input().split())
    tx, ty = map(int, input().split())
    q = deque()
    q.append((sx, sy))
    arr[sx][sy] = 0
    while len(q) > 0:
        cx, cy = q.popleft()
        if cx == tx and cy == ty:
            break
        for tdx, tdy in zip(dx, dy):
            nx, ny = cx + tdx, cy + tdy
            if 0 <= nx < M and 0 <= ny < M and not arr[nx][ny]:
                arr[nx][ny] = arr[cx][cy] + 1
                q.append((nx, ny))
    print(arr[tx][ty])
 

 

주석 추가

import sys
from collections import deque
 
input = sys.stdin.readline  # 입력 효율화
 
N = int(input())  # TC갯수
dx = [-1, -2, -2, -1, 1, 2, 2, 1]  # 나이트가 이동할 수 있는 X좌표
dy = [-2, -1, 1, 2, 2, 1, -1, -2]  # 나이트가 이동할 수 있는 Y좌표
 
for _ in range(N):
    M = int(input())  # 체스판의 크기
    arr = [[False for i in range(M)] for j in
           range(M)]  # 체스판의 크기만큼 2차원 배열 선언 (초기값: False) (나이트로 이동 가능한 최소 이동 횟수로 값이 저장됨)
    sx, sy = map(int, input().split())  # 나이트의 시작 위치
    tx, ty = map(int, input().split())  # 나이트의 목표 위치
    q = deque()  # BFS를 위한 Queue
    q.append((sx, sy))  # 시작위치 삽입
    arr[sx][sy] = 0  # 시작위치의 값을 0으로 초기화
    while len(q) > 0:  # Queue에 원소가 있다면
        cx, cy = q.popleft()  # 현재 위치를 pop
        if cx == tx and cy == ty:  # 현재 위치가 목표 위치라면
            break  # 반복문 중단
        for tdx, tdy in zip(dx, dy):  # 나이트가 갈 수 있는 다음 위치 변화량
            nx, ny = cx + tdx, cy + tdy  # 나이트의 다음 위치를 지정
            if 0 <= nx < M and 0 <= ny < M and not arr[nx][ny]:  # 다음 위치가 체스판 안에 있고, 값이 False(아직 방문하지 않은 상태)라면
                arr[nx][ny] = arr[cx][cy] + 1  # 해당 위치의 값을 현재 위치의 값 + 1로 저장
                q.append((nx, ny))  # Queue에 다음 위치 추가
    print(arr[tx][ty])  # 목표위치로 가는 최소 이동 횟수 출력

---

실행 결과