| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 우선순위 큐
- LRU
- 에라토스테네스의체
- 해시맵
- N-Queen
- 플루이드-워셜
- 좌표 정렬하기
- boj
- Flatten
- 백만 장자 프로젝트
- 다리놓기
- 회의실 배정
- 터렛
- BFS
- 다이나믹프로그래밍
- 브루트포스
- D2
- 간단한 369게임
- 스도쿠 검증
- 그리디 알고리즘
- firebase
- SWEA
- D3
- 투포인터
- 최단경로
- 나는야 포켓몬 마스터 이다솜
- 완전탐색
- 이분탐색
- 배포
- dfs
- Today
- Total
허비의 기술블로그
[BOJ] 키 순서(2458) - C++ 본문
1 ~ N 번의 번호가 붙은 학생이 있다. 두 학생끼리 키를 비교한 결과가 주어지는데, 이 결과를 통해서 본인의 키 순서를 알 수 있는 학생이 몇 명인지 구하는 문제이다. (단, 모든 학생의 키는 다르다.)
2458번: 키 순서
1번부터 N번까지 번호가 붙여져 있는 학생들에 대하여 두 학생끼리 키를 비교한 결과의 일부가 주어져 있다. 단, N명의 학생들의 키는 모두 다르다고 가정한다. 예를 들어, 6명의 학생들에 대하여
www.acmicpc.net
풀이 과정
학생의 키가 몇 번째인 지 알려면 그 학생은 대소 관계에 있어서 모든 학생과 연결돼 있어야 한다. 즉 모든 학생을 노드로 하고, (키가 작은 학생 -> 키가 큰 학생)으로 노드를 연결한다고 했을 때, 모든 학생과 연결돼 있다면, 그 학생의 키 순서를 알 수 있다. 이를 위해서는 주어지는 두 학생의 키 대소 관계를 바탕으로 다른 학생과 연결해야 한다.
ex)
case 1:
input :
3 3
1 2
3 1
3 - > 1 -> 2로 연결할 수 있고, 세 학생 모두 다른 학생과 연결돼 있으며, 키 순서를 알 수 있다.
case 2:
input:
6 4
1 2
2 4
2 5
5 6
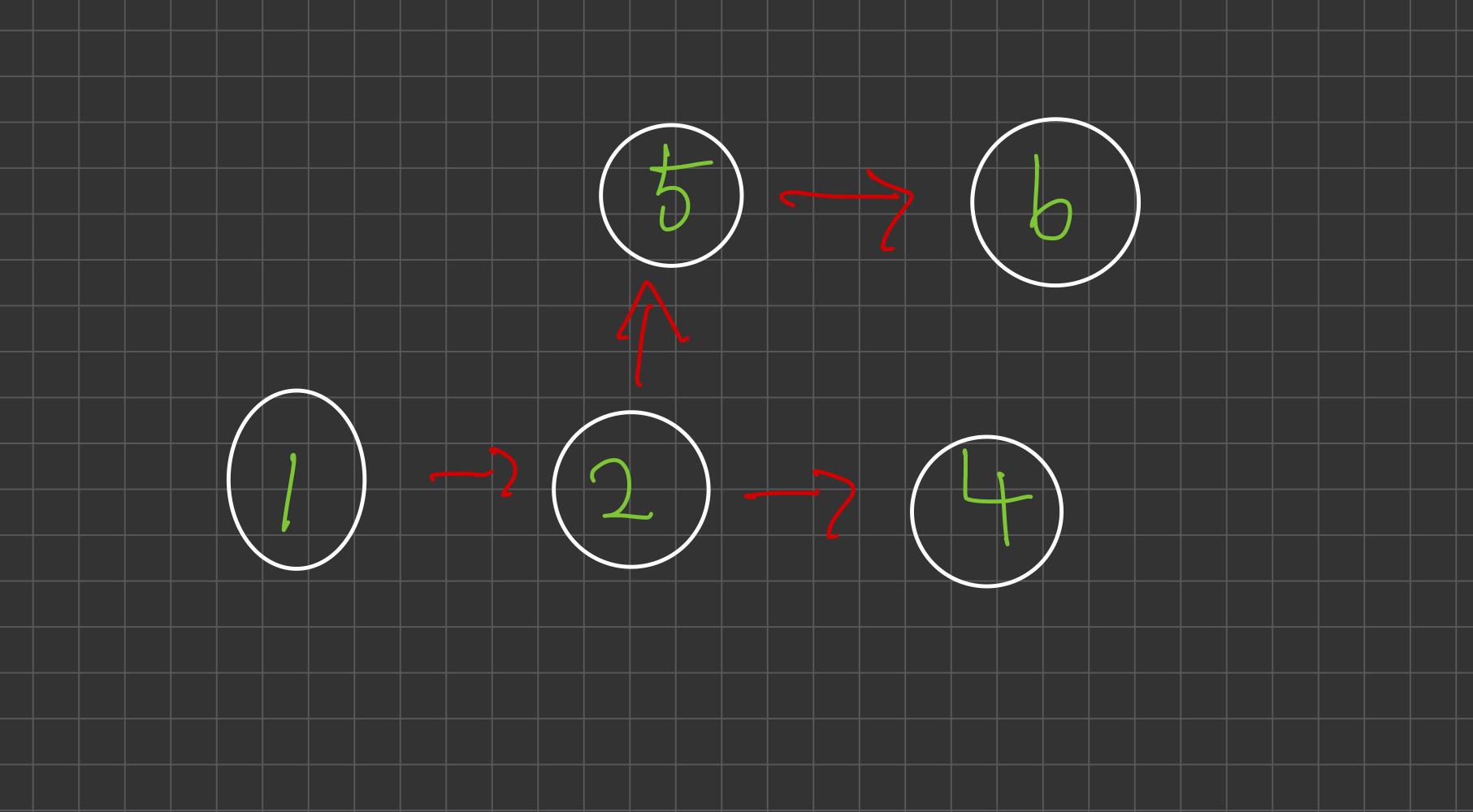
위 그림과 같이 연결할 수 있으며 1, 2 의 키 순서를 알 수 있다. (5, 6번은 4번 학생과의 키 관계를 알 수 없으므로 세 학생의 키 순서를 정확히 알 수 없다.)
이처럼 주어진 연결 정보를 통해 다른 정점으로 연결을 확장한 다음에, 자신을 제외한 모든 정점과 연결돼있는지 확인하면 된다. 다른 정점으로 연결을 확장하는 데는 '플로이드-워셜 알고리즘'을 활용한다.
플로이드-워셜 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 컴퓨터 과학에서 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)은 변의 가중치가 음이거나 양인 (음수 사이클은 없는) 가중 그래프에서 최단 경로들을 찾는 알고
ko.wikipedia.org
플로이드-워셜 알고리즘은 모든 정점에서 다른 모든 정점 간의 거리를 구하는 알고리즘이다. 여기서는 연결 여부를 검사하면 되므로 배열의 값으로 거리 대신 연결 여부(True / False)를 넣는다.
이렇게 플로이드-워셜 알고리즘으로 모든 정점간의 연결 여부가 나오게 되면, 각 정점마다 반복하며 다른 모든 정점들과 연결돼 있는지 확인한다. 이후 모든 정점과 연결된 정점의 개수를 정답으로 출력한다.
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <iostream>
#define MAXN 501
using namespace std;
bool arr[MAXN][MAXN] = { false };
int main(void) {
int N, M;
int a, b;
int ans = 0;
cin >> N >> M;
for (int i = 0; i < M; i++) {
cin >> a >> b;
arr[a][b] = true;
}
for (int k = 1; k <= N; k++) {
for (int i = 1; i <= N; i++) {
if (k == i)
continue;
for (int j = 1; j <= N; j++) {
arr[i][j] = (arr[i][j] | (arr[i][k] & arr[k][j]));
}
}
}
for (int i = 1; i <= N; i++) {
bool flag = true;
for (int j = 1; j <= N; j++) {
if (i == j || arr[i][j] || arr[j][i])
continue;
else {
flag = false;
break;
}
}
if (flag) {
ans++;
}
}
cout << ans << endl;
}
|
cs |
주석추가
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
#include <iostream>
#define MAXN 501
using namespace std;
bool arr[MAXN][MAXN] = { false }; // 연결 여부를 저장할 배열
int main(void) {
int N, M; // 학생의 수, 비교 횟수
int a, b; // 키가 작은 학생, 키가 큰 학생
int ans = 0; // 정답
cin >> N >> M;
for (int i = 0; i < M; i++) {
cin >> a >> b;
arr[a][b] = true; // 키가 작은 학생 -> 키가 큰 학생 연결하기
}
//플로이드-워셜 알고리즘
for (int k = 1; k <= N; k++) { //k:경유지, 경유지가 1 ~ N 까지
for (int i = 1; i <= N; i++) { // 시작 위치
if (k == i) // 시작위치와 경유지가 같다면 pass
continue;
for (int j = 1; j <= N; j++) { // 끝 위치
arr[i][j] = (arr[i][j] | (arr[i][k] & arr[k][j])); // 시작위치와 끝 위치 연결 정보 갱신
}
}
}
//각 정점별로 다른 모든 정점과 연결돼있는지 확인
for (int i = 1; i <= N; i++) {
bool flag = true;
for (int j = 1; j <= N; j++) {
if (i == j || arr[i][j] || arr[j][i]) // i와 j가 같은 노드이거나, i -> j, j -> i 중 연결 돼 있는 방향이 있다면
continue;
else { //연결돼 있지 않다면
flag = false;
break;
}
}
if (flag) {
ans++; //반복을 다 돌았는데 모든 정점과 연결 돼 있다면 정답 + 1
}
}
cout << ans << endl;
}
|
cs |
정점 간 연결 여부는 bool 값을 통해 True / False로 계산했다. 25번째 라인(주석 추가 26번째 라인)의 연결 정보 갱신 과정은 비트 연산을 통해 계산했다.
| : or 연산
& : and 연산arr[i][j]가 이미 true였던 경우 뒤의 값과 상관없이 arr[i][j]가 true로 갱신되며, arr[i][j]가 false 였다면, arr[i][k]와 arr[k][j]가 모두 true 여야 arr[i][j]가 true로 갱신된다.
실행 결과

'BOJ' 카테고리의 다른 글
| [BOJ] 알파벳(1987) - C++ (0) | 2022.09.29 |
|---|---|
| [BOJ] 소수의 연속합(1644) - PYTHON (0) | 2022.08.15 |
| [BOJ] 오르막 수(11057) - PYTHON (0) | 2022.06.29 |
| [BOJ] 치킨 배달(15686) - PYTHON (0) | 2022.06.27 |
| [BOJ] 부분수열의 합(1182) - PYTHON (0) | 2022.06.26 |


